콘텐츠
지오메트리에서 삼각형은 3 개의 각도를 이루도록 연결되는 3 개의 변이있는 모양입니다. 삼각형의 모든 각도의 합은 180도이므로 다른 두 각도를 알고 있으면 항상 삼각형에서 한 각도의 값을 찾을 수 있습니다. 이 작업은 3 개의 등변과 각도가있는 등변 및 2 개의 등변과 각도가있는 이등변과 같은 특수 삼각형의 경우 더 쉽습니다. 또한 변의 길이와 면적과 같은 삼각형의 속성을 결정하는 데 도움이되는 삼각형 공식을 아는 것이 도움이됩니다.
직각 삼각형의 계산
피타고라스 정리를 기억하십시오. 피타고라스 정리를 사용하여 양변의 길이를 알고 있다면 직각 삼각형의 변의 길이를 계산할 수 있습니다. 또한 정리가 만족되는 경우 삼각형이 직각 (90도)인지를 확인할 수 있습니다. a ^ 2 + b ^ 2 = c ^ 2 ( "a"제곱 더하기 "b"제곱은 "c"제곱, 여기서 "c"는 삼각형의 가장 긴 변과 직각의 반대쪽입니다.)
알고있는 삼각형 변의 길이를 입력하십시오. 예를 들어, 한쪽 (a)가 2이고 다른 쪽 (b)가 5 인 삼각형의 빗변의 길이 (오른쪽 삼각형의 가장 긴 변)를 찾으라는 메시지가 표시되면 다음 방정식으로 가정하십시오 : 2 ^ 2 + 5 ^ 2 = c ^ 2.
대수를 사용하여 "c"의 값을 찾으십시오. 2 ^ 2 + 5 ^ 2 = c ^ 2는 4 + 25 = c ^ 2가됩니다. 그러면 29 = c ^ 2가됩니다. 답 c는 29 또는 5.4의 제곱근이며 가장 가까운 10 분의 1로 반올림됩니다. 삼각형이 직각 삼각형인지 여부를 묻는 메시지가 표시되면 삼각형의 길이를 피타고라스 정리에 입력하십시오. a ^ 2 + b ^ 2가 실제로 c ^ 2와 같으면 삼각형은 직각 삼각형입니다. 등호의 양쪽에서 방정식의 균형이 맞지 않으면 직각 삼각형이 될 수 없습니다.
삼각형의 면적을 계산
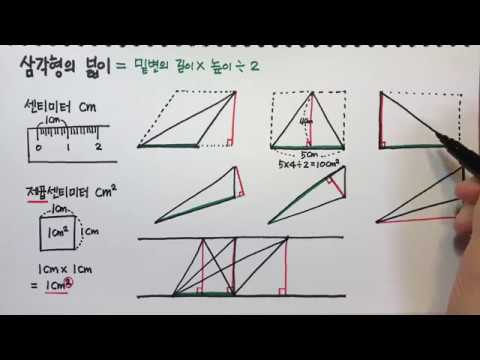
삼각형의 면적에 대한 방정식을 사용하십시오. 삼각형의 기본 시간 높이의 절반에 해당하는 삼각형을 알면 삼각형의 면적을 찾을 수 있습니다. 방정식은 A = (1/2) bh이며, 여기서 b (기본)는 삼각형의 가로 길이이고 h (높이)는 삼각형의 세로 길이입니다. 삼각형이 바닥에 앉아 있다고 상상하면 바닥은 바닥에 닿는면이고 높이는 위로 뻗은면입니다.
삼각형의 길이를 방정식에 대입합니다. 예를 들어, 삼각형의 밑면이 3이고 높이가 6 인 경우, 면적에 대한 방정식은 A = (1/2) _3_6 = 9가됩니다. 또는 삼각형의 면적과 밑면이 주어지고 높이를 찾으려면 알려진 값을이 방정식으로 대체 할 수 있습니다.
대수를 사용하여 방정식을 풉니 다. 삼각형의 면적이 50이고 높이가 10이라는 것을 알고 있다고 가정하면 어떻게 기초를 찾을 수 있습니까? 삼각형 면적 A = (1/2) bh에 대한 방정식을 사용하여 값을 대체하여 50 = (1/2) _b_10을 얻습니다. 방정식의 우변을 간단히하면 50 = b * 5가됩니다. 그런 다음 방정식의 양변을 5로 나누면 b의 값인 10이됩니다.