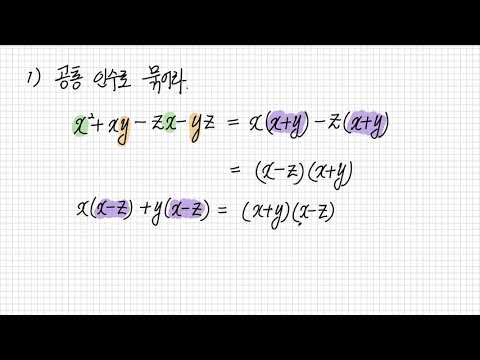
다항식은 변수와 상수를 포함하는 수학 방정식입니다. 또한 지수가있을 수 있습니다. 상수와 변수는 덧셈으로 결합되는 반면, 상수와 변수가있는 각 항은 덧셈 또는 뺄셈으로 다른 항에 연결됩니다. 다항식 인수 분해는 나눗셈으로 표현을 단순화하는 과정입니다. 다항식을 인수 분해하려면 이항식인지 삼항식인지 판별하고, 표준 인수 분해 형식을 이해하고, 가장 큰 공통 인수를 찾고, 다항식의 다양한 부분의 곱과 곱에 해당하는 숫자를 찾은 다음 대답.
다항식이 이항인지 삼항인지를 결정합니다. 이항에는 두 개의 항이 있고 삼항에는 세 개의 항이 있습니다. 이항의 예는 4x-12이고 삼항의 예는 x ^ 2 + 6x + 9입니다.
두 개의 완벽한 사각형의 차이, 두 개의 완벽한 큐브의 합 및 두 개의 완벽한 큐브의 차이의 차이점을 이해하십시오. 이 유형의 다항식은 이항식이며 인수 분해를위한 특수 형식이 있습니다. 예를 들어, x ^ 2-y ^ 2는 두 완벽한 제곱의 차이입니다. 각 항의 제곱근을 찾아서 괄호 세트에서 빼고 (x + y) (x-y)와 같이 다른 괄호로 묶어이를 인수 분해합니다. 다항식 x ^ 3-y ^ 3은 두 개의 완벽한 큐브의 차이입니다. 각 항의 세제곱근을 찾은 후 (x-y) (x ^ 2 + xy + y ^ 2) 형식으로 입력합니다. 두 개의 완벽한 큐브의 합은 x ^ 3 + y ^ 3입니다. 팩토링의 형식은 (x + y) (x ^ 2-xy + y ^ 2)입니다.
가장 큰 공통 요소를 찾으십시오. 최대 공약수는 다항식의 모든 상수로 나눌 수있는 가장 큰 수입니다. 예를 들어, 4x-12에서 가장 큰 공통 요소는 4입니다. 4를 4로 나눈 값은 1이고 12를 4로 나눈 값은 3입니다. 4 개를 빼면이 식은 4 (x-3)로 단순화됩니다.
곱에 해당하는 숫자와 다항식의 두 번째 및 세 번째 항의 합계를 찾습니다. 이것은 삼항식을 고려하는 방법입니다. 예를 들어 x ^ 2 + 6x + 9 문제에서 세 번째 항 9에 더해지는 두 개의 숫자와 두 번째 항에 곱하는 두 개의 숫자 6을 찾아야합니다. 숫자는 3 * 3 = 9 및 3 + 3 = 6과 같이 3과 3입니다. 다항식 인수는 (x + 3) (x + 3)입니다.
답을 확인하십시오. 다항식을 올바르게 인수 분해하려면 답의 내용을 곱하십시오. 예를 들어, 답 4 (x-3)의 경우, 4에 x를 곱한 다음 4x-12와 같이 3을 네 번 뺍니다. 4x-12는 원래 다항식이므로 답이 맞습니다. 답 (x + 3) (x + 3)의 경우 x에 x를 곱한 다음 x에 3을 더한 다음 x에 3을 더한 다음 3을 3 번 더하거나 x ^ 2 + 3x + 3x + 이는 x ^ 2 + 6x + 9로 단순화됩니다.