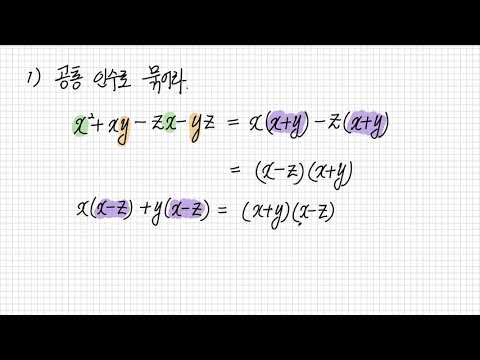
콘텐츠
다항식 또는 삼항식을 인수 분해하면이를 다항식으로 표현할 수 있습니다. 다항식과 삼항식을 인수 분해하면 0을 풀 때 중요합니다. 인수 분해를 사용하면 해를 더 쉽게 찾을 수있을뿐만 아니라 이러한 표현에는 지수가 포함되므로 여러 해가있을 수 있습니다. 다항식과 삼항식을 인수 분해하는 방법에는 여러 가지가 있으며 사용되는 방법은 다양합니다. 이러한 방법에는 그룹화 및 FOIL 방법을 사용하여 가장 일반적인 요인을 찾는 방법이 포함됩니다.
최대 공약수
다항식 또는 삼항식을 인수 분해하기 전에 최대 공약수 (있는 경우)를 검색합니다. 일반적으로 가장 빠른 방법은 소수를 사용하는 것입니다. 즉 소수를 사용하여 숫자를 곱으로 표현하는 것입니다. 일부 다항식에서 가장 큰 공약수에는 변수도 포함될 수 있습니다.
숫자 20과 30을 고려하십시오. 20의 소인수 분해는 2 x 2 x 5이고 30의 소인수 분해는 2 x 3 x 5입니다. 공통 요소는 2와 5입니다. 5와 10의 2 배가 10이므로 10이 가장 큰 공통 요소입니다.
곱하여 인수 분해 결과를 확인하십시오. 7x ^ 2 + 14-7 (x ^ 2 + 2) 식을 인수 분해 할 수 있습니다. 이 인수 분해를 곱하면 원래 식인 7x ^ 2 + 14로 돌아가므로 정확합니다.
그룹화
그룹화를 통해 인수 분해를 사용하여 4 개의 항으로 특정 다항식을 인수 분해합니다.
다항식 x ^ 3 + x ^ 2 + 2x + 2를 고려하십시오. 모든 항에 공통 인 것 이외의 다른 요인은 없습니다.
x ^ 3 + x ^ 2 및 2x + 2를 개별적으로 인수 분해합니다 : x ^ 3 + x ^ 2 = x ^ 2 (x + 1) 및 2x + 2 = 2 (x + 1). 따라서 x ^ 3 + x ^ 2 + 2x + 2 = x ^ 2 (x + 1) + 2 (x + 1) = (x ^ 2 + 2) (x + 1)입니다. 마지막 단계에서는 x + 1이 공통 요인이므로 x + 1을 분해합니다.
FOIL 방법
FOIL (첫 번째, 외부, 내부, 마지막) 방법을 사용하여 ax ^ 2 + bx + c 유형의 삼항을 인수 분해합니다. 인수 분해 된 삼항은 두 개의 이항으로 구성됩니다. 예를 들어, 식 (x + 2) (x + 5) = x ^ 2 + 5x + 2x + 2 (5) = x ^ 2 + 7x + 10입니다. 선행 계수 a가 1 인 경우 계수, b는 이항 항의 항 항 (이 경우 2와 5)의 합이며 삼항 항 c는 항의 곱입니다.
가장 큰 공통 요소가 있다면이를 밖으로 빼냅니다. a가 하나 또는 소수가 아닌 경우 계속하기 전에 가능한 모든 요인을 나열하여 a의 두 가지 요인을 찾으십시오. 각 숫자에 x를 곱하십시오. 이들은 각 이항의 첫 번째 용어입니다. 많은 삼항식에서 계수 a는 1과 같습니다. 예 3x ^ 2-10x-8을 고려하십시오. 공통 인자는 없으며 첫 번째 항의 유일한 가능성은 3x와 x입니다. 이것은 이항식의 첫 번째 항을 제공합니다 : (3x +) (x +).
c와 같은 수를 구하여 이항식의 마지막 항을 구합니다. 위의 예를 사용하면 마지막 항의 곱은 -8이어야합니다. 8과 -1, 2와 -4를 포함하여 -8에 대한 여러 가지 인수 분해가 있습니다. 계속하기 전에 가능한 모든 요인의 목록을 작성하십시오.
합이 bx 인 위 단계에서 생성 된 외부 및 내부 제품을 찾으십시오. 시행 착오를 사용하여 이전 단계에서 찾은 요인을 테스트합니다. FOIL 방법을 사용하여 답을 확인하십시오. (3x + 2) (x-4) = 3x ^ 2-12x + 2x-8 = 3x ^ 2-10x-8