
콘텐츠
형상에서 팔각형은 8 개의면이있는 다각형입니다. 정 팔각형은 8 개의 동일한 변과 같은 각도를 가지고 있습니다. 정 팔각형은 일반적으로 정지 신호에서 인식됩니다. 8 면체는 8 면체 다면체입니다. 정팔면체는 길이가 같은 모서리를 가진 8 개의 삼각형을 가지고 있습니다. 기지에서 만나는 2 개의 정사각형 피라미드입니다.
팔각형 면적 공식
길이 "a"의 변을 가진 정 팔각형의 면적에 대한 공식은 2 (1 + sqrt (2)) a ^ 2이며, 여기서 "sqrt"는 제곱근을 나타냅니다.
유도
팔각형은 사각형 4 개, 중앙 사각형 1 개, 모서리 이등변 삼각형 4 개로 볼 수 있습니다.
정사각형의 면적은 a ^ 2입니다.
삼각형은 피타고라스 정리에 의해 변 a, a / sqrt (2) 및 a / sqrt (2)를 갖습니다. 따라서 각각의 면적은 a ^ 2 / 4입니다.
직사각형은 면적 a * a / sqrt (2)입니다.
이 9 개 영역의 합은 2a ^ 2 (1 + sqrt (2))입니다.
정팔면체 볼륨 공식
측면 "a"의 정팔면체의 부피 공식은 a ^ 3 * sqrt (2) / 3입니다.
유도
4면 피라미드의 면적은 기본 * 높이 / 3의 면적입니다. 따라서 정규 팔각형의 면적은 2 * 기본 * 높이 / 3입니다.
기본 = a ^ 2
"F"와 "C"라고하는 두 개의 인접한 정점을 선택하십시오. "O"가 중앙에 있습니다. FOC는 밑변이 "a"인 이등변 직각 삼각형이므로 OC와 OF의 길이는 피타고라스 정리에 의해 a / sqrt (2)입니다. 따라서 높이 = a / sqrt (2).
따라서 정팔면체의 부피는 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3입니다.
표면적
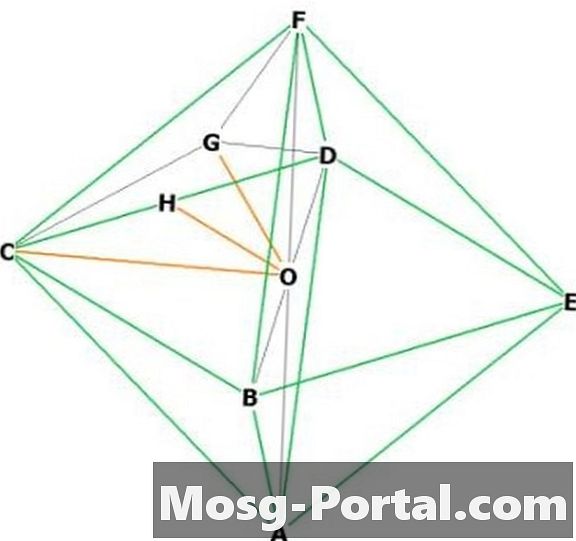
정팔면체 표면은 측면 "a"의 정삼각형의 면적에 8 개의면이있다.
피타고라스 정리를 사용하려면 정점에서 밑면으로 선을 놓습니다. 이렇게하면 길이 "a"와 한 변의 길이 "a / 2"를 갖는 두 개의 직각 삼각형이 만들어집니다. 따라서 세 번째면은 sqrt = sqrt (3) a / 2 여야합니다. 따라서 정삼각형의 면적은 높이 * 기준 / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2 / 4입니다.
8면의 경우, 정팔면체의 표면적은 2 * sqrt (3) * a ^ 2입니다.