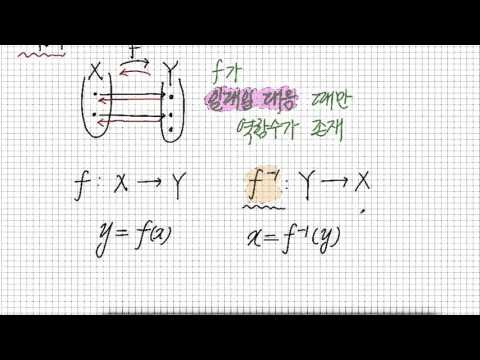
콘텐츠
수학에서 역함수를 찾으려면 먼저 함수가 있어야합니다. 종속 변수 y에 대한 값을 생성하는 독립 변수 x에 대한 거의 모든 연산 세트 일 수 있습니다. 일반적으로, x의 역함수를 구하려면 함수에서 y를 x로 바꾸고 x를 y로 바꾸고 x를 구하십시오.
TL; DR (너무 길고 읽지 않음)
일반적으로, x의 역함수를 구하려면 함수에서 x를 y로 대체하고 x를 y로 대체 한 다음 x를 구하십시오.
역함수 정의
함수의 수학적 정의는 x 값에 대해 y 값이 하나만 존재하는 관계 (x, y)입니다. 예를 들어, x의 값이 3 인 경우 y에 10과 같은 값이 하나만 있으면 관계가 함수입니다. 역함수는 원래 함수의 y 값을 고유 한 x 값으로 사용하여 y 값을 생성합니다. 이것이 원래 함수의 x 값입니다. 예를 들어, x 변수의 값이 0, 1 및 2 일 때 원래 함수가 y 값 1, 3 및 10을 반환 한 경우 x 변수의 값이 1 인 경우 역함수는 y 값 0, 1 및 2를 반환합니다. 본질적으로 역함수는 원본의 x와 y 값을 바꿉니다. 수학 언어에서 원래 함수가 f (x)이고 역이 g (x)이면 g (f (x)) = x입니다.
역함수에 대한 대수 접근법
두 변수 x와 y를 포함하는 함수의 역함수를 찾으려면 x 항을 y로 바꾸고 y 항을 x로 바꾸고 x를 구하십시오. 예를 들어, 선형 방정식 y = 7x-15를 사용하십시오.
y = 7x-15 원래 기능
x = 7y-15 y를 x로 바꾸고 x를 y로 바꾸십시오.
x + 15 = 7y-15 + 15 양변에 15를 더합니다.
x + 15 = 7y 단순화
(x + 15) / 7 = 7y / 7 양변을 7로 나눕니다.
(x + 15) / 7 = y 단순화
함수 (x + 15) / 7 = y는 원본의 역함수입니다.
역삼 각 함수
삼각 함수의 역수를 구하려면 모든 삼각 함수와 그 역수에 대해 알아야합니다. 예를 들어, y = sin (x)의 역을 찾으려면 사인 함수의 역함수가 아크 사인 함수라는 것을 알아야합니다. arcsin (x) 없이는 간단한 대수는 없습니다. 코사인, 탄젠트, 코시컨트, 시컨트 및 코탄젠트와 같은 다른 삼각 함수는 각각 아크 코사인, 아크 탄젠트, 아크 코시컨트, 아크 섹탄 및 아크 코탄젠트의 역함수를 갖습니다. 예를 들어, y = cos (x)의 역수는 y = arccos (x)입니다.
함수와 역의 그래프
함수와 그 역의 그래프가 흥미 롭습니다. 두 개의 곡선을 플로팅 한 다음 y = x 함수에 해당하는 선을 그리면 선이 "미러"로 나타납니다. y = x 아래의 곡선 또는 선은 그 위에 대칭으로 "반사"됩니다. 다항식, 삼각법, 지수 또는 선형에 관계없이 모든 함수에 적용됩니다. 이 원리를 사용하면 원래 함수를 그래프로 표시하고 y = x에서 선을 그린 다음 y = x를 축으로하는 "미러 이미지"를 만드는 데 필요한 곡선 또는 선을 그려 함수의 역수를 그래픽으로 설명 할 수 있습니다. 대칭.