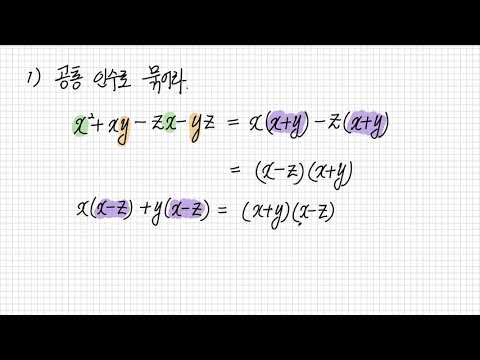
콘텐츠
거의 모든 학생이 처음 만났을 때 어려움을 겪고있는 수학 과목이 하나라도 있다면 대수학, 특히 삼항식의 인수 분해입니다. 삼항식을 인수 분해하는 방법에는 여러 가지가 있으며 그중 누구도 "쉬운"이라고 부르는 방법은 없습니다. 그러나 각각은 일관된 연구와 실습으로 이해할 수 있습니다.
삼항이란 무엇입니까?
먼저 다항식이 무엇인지 알아야합니다. 다항식은 3x 및 5y와 같은 항, 숫자 및 변수의 조합을 갖는 대수 방정식입니다. 다항식의 일부 예는 2x + 3, 3xy-4y 및 3x + 4xy-5y입니다. 마지막 예를 삼항이라고합니다. 삼항은 3 항의 다항식입니다.
최대 공약수
삼항식을 인수 분해하는 첫 번째 방법 인 "가장 쉬운"방법은 가장 큰 공통 인수, 즉 세 항이 공통적으로 갖는 가장 큰 수, 변수 또는 항을 찾는 것입니다. 예를 들어, 삼항식 2x ^ 2 + 6x + 4의 경우 숫자 2는 세 항 모두 공통 인 숫자이므로 2를 빼면 2 (x ^ 2 + 3x + 2)가됩니다. 괄호 안의 삼항은 실제로 더 고려 될 수 있습니다.
이차 삼항식의 인수 분해
삼항식 x ^ 2 + 3x + 2는 2의 거듭 제곱을 갖는 항을 갖기 때문에 2 차 삼항식입니다. 이 다항식을 고려하려면 2 차법에 대한 규칙을 알아야합니다. 첫째, 이차 삼항식의 요인은 일반적으로 x + 2 또는 2y-3과 같은 두 개의 이항 법입니다. 둘째, 이차 삼항식의 첫 번째 항은 두 이항의 첫 항의 곱입니다. 셋째, 이차 삼항의 마지막 항은 두 이항의 마지막 항의 곱입니다. 넷째, 2 차 삼항식의 중간 항의 계수는 두 이항의 마지막 항의 합입니다. 다섯째, 이차 삼항의 모든 부호가 양수이면 두 이항의 모든 부호는 양수입니다.
팩토링 예
2 차 삼항 x ^ 2 + 3x + 2를 인수 분해하려면 두 세트의 괄호 () ()로 시작하십시오. 두 번째 괄호 (x) (x)에 x를 써서 두 번째 단계를 수행하십시오. 변수 x ^ 2는 x에 x를 곱한 값과 같으며 첫 번째 규칙을 이행합니다. 세 번째 단계는 삼항식의 마지막 항이 두 이항식의 마지막 항의 곱이므로 마지막은 1과 2 또는 -1과 -2 여야하며 둘 다 동일해야합니다. 항 계수는 두 이항의 마지막 항의 합입니다. 1과 2 만 3과 같으므로 솔루션은 (x + 1) (x + 2)입니다. 또한 다섯 번째 규칙도 만족합니다.
특수 사례 및 기타 정보
때로는 팩토링을 쉽게하기 위해 삼항을 다시 작성해야 할 수도 있습니다. 삼항식 3x + 2y + 3xy는 3x + 3xy + 2y의 논리적 인 순서로 풀기 쉬운 용어와 함께 풀기가 더 쉽습니다. 삼항식의 순서를 재정렬하는 것은 삼항식의 모든 부호가 양수인 경우에만 사용할 수 있습니다. 또한 x ^ 2 + 4x +2와 같은 일부 삼항식은 인수 분해 할 수 없습니다. 이 삼항을 더 이상 세분화 할 수있는 방법은 없습니다.