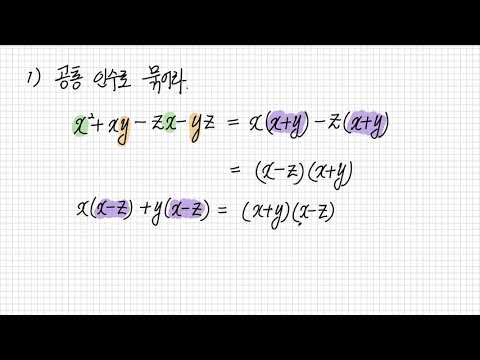
콘텐츠
대수학에서 인수 분해는 2 차 방정식 또는 표현을 단순화하는 가장 기본적인 방법 중 하나입니다. 교사와 책은 종종 기본 대수 수업에서 그 중요성을 강조하며, 정당한 이유가 있습니다. 학생들이 대수학을 깊고 깊게 파고 들자 마자 동시에 여러 이차 표현을 다루는 것을 알게 될 것입니다. 단순화되면 해결하기가 훨씬 쉬워집니다.
식의 첫 번째 및 마지막 항에 정수를 곱하여 식의 키 번호를 찾으십시오. 예를 들어, 식 2x에서2 + x – 6, 2와 -6을 곱하여 -12를 얻습니다.
중기 적으로 합산되는 키 번호의 요인을 계산합니다. 위에 주어진 식을 사용하면 중간에 단 하나의 항만 있기 때문에 곱셈이 -12 일뿐만 아니라 합이 1 인 두 개의 숫자를 찾아야합니다. 이 경우 4 × -3 = -12 및 4 + (-3) = 1이므로 숫자는 -12와 1입니다.
2 × 2 격자를 만들고 왼쪽 위와 오른쪽 아래에 각각 첫 번째와 마지막 항을 입력합니다. 위의 표현에서 첫 번째와 마지막 용어는 2x입니다.2 및 -6.
변수를 포함하여 그리드의 다른 두 상자 중 하나에 두 가지 요인을 입력하십시오. 위에서 주어진 식에서 인수는 4와 -3이며 그리드의 다른 두 상자에 4x와 -3x로 입력합니다.
두 행 각각의 숫자가 공유하는 공통 요소를 찾으십시오. 위에서 주어진 식에서 첫 번째 행의 숫자는 2x와 -3x이며 공통 요소는 x입니다. 두 번째 행에서 숫자는 4x와 -6이며 공통 요소는 2입니다.
두 열 각각의 숫자가 공유하는 공통 요소를 찾으십시오. 위의 식에서 첫 번째 열의 숫자는 2x입니다.2 -4 배이며 공통 요인은 2 배입니다. 두 번째 열의 숫자는 -3x와 -6이며 공통 요소는 -3입니다.
행과 열에서 찾은 공통 요인을 기반으로 두 가지 표현식을 작성하여 인수 분해 표현식을 완성하십시오. 위의 예에서 행은 x와 2의 공통 요소를 산출하므로 첫 번째 표현식은 (x + 2)입니다. 열이 2x와 -3의 공통 요인을 산출하므로 두 번째 표현은 (2x-3)입니다. 따라서 최종 결과는 (2x-3) (x + 2)이며, 이는 원래 표현식의 요인 버전입니다.
팩토링을 다시 확인하는 방법
FOIL 순서를 사용하여 요인 항을 곱하여 새로 인수 분해 된 표현식을 다시 확인할 수 있습니다. 그것은 첫 번째 용어, 외부 용어, 내부 용어 및 마지막 용어를 의미합니다. 수학을 올바르게 수행했다면, FOIL 곱셈의 결과는 시작한 원래의 인수 분해되지 않은 표현이어야합니다.
다항식 계산기 (참고 자료 참조)에 원래 식을 입력하여 자신의 계산 결과를 다시 확인할 수있는 일련의 요소를 반환하여 인수 분해를 다시 확인할 수도 있습니다. 그러나이 유형의 계산기는 빠른 스팟 확인에 유용하지만 대수적 표현을 직접 고려하는 방법을 배우는 대신 사용할 수는 없습니다.