콘텐츠
"사인"은 분수로 표현 된 직각 삼각형의 두 변의 비율에 대한 수학 속기입니다. 측정하는 각도와 반대되는 변은 분수의 분자이고 직각 삼각형의 빗변은 분모입니다. 일단이 개념을 숙달하면 죄의 법칙으로 알려진 공식의 구성 요소가됩니다.이 법칙은 각도의 2 개 이상, 한쪽 또는 2 개 이상을 알고있는 한 삼각형의 누락 된 각도와 측면을 찾는 데 사용할 수 있습니다. 측면과 하나의 각도.
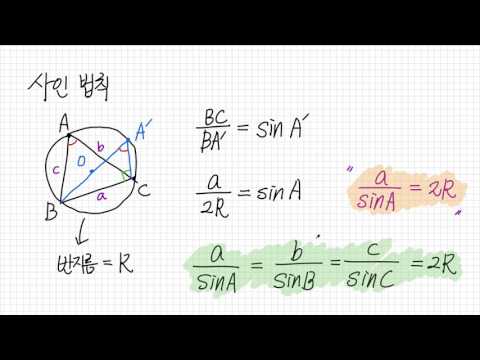
사인의 법칙을 다시 정의
죄의 법칙에 따르면 삼각형의 각도와 반대쪽의 비율은 삼각형의 세 가지 각도에 대해 동일합니다. 또는 다른 방법으로 말하면 :
죄 (A) /에이 = 죄 (B) /비 = 죄 (C) /씨, 여기서 A, B 및 C는 삼각형의 각도입니다. a, b 과 씨 그 각도에 반대되는 변의 길이입니다.
이 형식은 누락 된 각도를 찾는 데 가장 유용합니다. 당신이 죄의 법칙을 사용하여 삼각형의 한 변의 길이를 잃어 버렸다면, 그것을 분모에있는 죄와 함께 쓸 수도 있습니다 :
에이/ sin (A) = 비/ sin (B) = 씨/ sin (C)
사인의 법칙으로 누락 된 각도 찾기
알려진 각도가 하나 인 삼각형이 있다고 가정합니다. 각도 A의 각도는 30 도입니다. 또한 삼각형의 두 변의 측도를 알고 있습니다. 에이반대 각도 A 인, 4 단위 및 측면 측정 비 6 단위를 측정합니다.
알려진 모든 정보를 죄의 법칙의 첫 번째 형태로 입력하십시오. 이는 누락 된 각도를 찾는 데 가장 좋습니다.
sin (30) / 4 = sin (B) / 6 = sin (C) /씨
다음으로 목표를 선택하십시오. 이 경우 각도 B의 측정 값을 찾으십시오.
문제를 설정하는 것은이 방정식의 첫 번째와 두 번째 표현식을 서로 동일하게 설정하는 것만 큼 간단합니다. 지금 세 번째 용어에 대해 걱정할 필요가 없습니다. 따라서, 당신은 :
sin (30) / 4 = 죄 (B) / 6
알려진 각도의 사인을 찾으려면 계산기 나 차트를 사용하십시오. 이 경우 sin (30) = 0.5이므로 다음을 갖습니다.
(0.5) / 4 = sin (B) / 6 : 다음을 단순화합니다.
0.125 = sin (B) / 6
방정식의 각 변에 6을 곱하여 알 수없는 각도의 사인 측정 값을 분리합니다. 이것은 당신에게 제공합니다 :
0.75 = 죄 (B)
계산기 나 표를 사용하여 알 수없는 각도의 역 사인 또는 아크 사인을 찾으십시오. 이 경우 0.75의 역 사인은 약 48.6 도입니다.
경고
사인의 법칙으로 측면 찾기
알려진 각도가 15도 및 30 도인 삼각형 (각각 A와 B라고 함)과 변의 길이가 있다고 가정합니다 에이각도 A와 반대 인 길이는 3 단위입니다.
앞에서 언급했듯이 삼각형의 세 가지 각도는 항상 최대 180 도입니다. 따라서 두 각도를 이미 알고 있다면 알려진 각도를 180에서 빼서 세 번째 각도의 측정 값을 찾을 수 있습니다.
180-15-30 = 135도
따라서 누락 된 각도는 135 도입니다.
두 번째 형식을 사용하여 이미 알고있는 정보를 sines 공식에 기입하십시오 (결 측값을 계산할 때 가장 쉬운 방법).
3 / sin (15) = 비/ sin (30) = 씨/ sin (135)
길이를 찾을 누락 된면을 선택하십시오. 이 경우 편의상 측면의 길이를 찾으십시오. 비.
문제를 설정하기 위해 죄의 법칙에 주어진 두 가지 사인 관계를 선택합니다. 비) 및 이미 알고있는 모든 정보 (그쪽 에이 및 각도 A). 이 두 사인 관계를 서로 동일하게 설정하십시오.
3 / sin (15) = 비/ sin (30)
이제 해결 비. 계산기 또는 표를 사용하여 sin (15) 및 sin (30)의 값을 찾아 방정식에 채우십시오 (이 예에서는 0.5 대신 분수 1/2 사용). :
3/0.2588 = 비/(1/2)
선생님은 사인 값을 얼마나 멀리 올릴 수 있는지 알려 줄 것입니다. 또한 sin (15)의 경우 매우 지저분한 (√6 – √2) / 4 인 사인 함수의 정확한 값을 사용하도록 요청할 수도 있습니다.
다음으로 방정식의 양변을 단순화하고 분수로 나누는 것은 그 역수를 곱하는 것과 같습니다.
11.5920 = 2_b_
변수는 일반적으로 왼쪽에 나열되므로 편의상 방정식의 측면을 전환하십시오.
2_b_ = 11.5920
그리고 마지막으로 비. 이 경우 방정식의 양변을 2로 나누면됩니다.
비 = 5.7960
따라서 삼각형의 누락 된 변의 길이는 5.7960 단위입니다. 같은 절차를 사용하여 쉽게 해결할 수 있습니다. 씨죄의 법칙에서 그 용어를 측면의 용어와 동일하게 설정 에이, 이미 해당 측면에 대한 전체 정보를 알고 있기 때문입니다.