콘텐츠
이등변 삼각형에는 두 개의 동일한 변이 있습니다. 면적은 삼각형 내 총 공간입니다. 삼각형 화단에 얼마나 많은 뿌리 덮개를 넣을 것인지, A- 라인 건물의 앞면을 덮는 데 필요한 페인트의 양을 결정하거나, 기술을 연마하기 위해 단순히 드릴링 해야하는 경우 삼각형 영역에 알고있는 것을 연결하십시오. 공식.
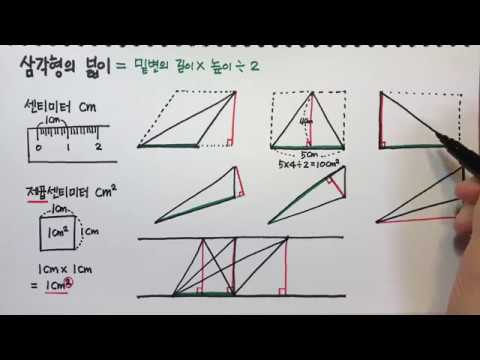
공식
이등변 삼각형의 면적을 찾으려면 밑면 또는 삼각형의 아래쪽 너비와 가슴 가장 높은 지점의 높이를 곱한 다음 제품을 반으로 나눕니다. 밑면은 밑면이거나 다른 두면과 같지 않은면입니다. 높이는 삼각형의 가장 높은 피크에서 두 짝이 만나는 지점에서 밑면까지의 거리입니다. 공식은 A = ½ x b x h여기서 b는 밑이고 h는 높이입니다.
연결
값을 공식에 연결하여 면적을 찾으십시오. 밑변과 높이를 곱한 다음 2로 나눕니다. 예를 들어, 삼각형의 밑변이 8이고 높이가 9이면 수식은 다음과 같습니다. 면적 = (½)(8)(9) = 36. 밑면이 7이고 높이가 3이면 면적은 (½)(7)(3). 10.5의 면적으로 21을 2로 나눕니다.
피타고라스의 정리
피타고라스 정리를 사용하여 밑면 또는 높이를 찾아야 할 수도 있습니다. 이등변 삼각형의 두 반쪽은 두 개의 직각 삼각형을 형성합니다. 높이를 나타내는 선은 이등변 삼각형을 아래쪽에서 끝으로 반으로 나누고 밑면과 직각을 만듭니다. 이 오른쪽 삼각형 중 하나를 보면 이등변 삼각형의 높이는 다리 중 하나가되고 이등변 밑면의 절반은 다른 다리가되고 이등변 삼각형의 변은 빗변이됩니다. 피타고라스 정리 공식은 에이2 + b2 = c2여기서 a와 b는 직각 삼각형의 다리이고 c는 빗변입니다. a 또는 b를 해결하여 높이를 찾는 데 사용할 수 있습니다. a 또는 b를 풀면 밑을 찾을 수 있습니다.직각 삼각형의 다리가 이등변 삼각형의 밑면의 절반에 불과하기 때문에 기본 솔루션에 2를 곱하여 전체 기본 측정 값을 얻습니다.
피타고라스 응용
변의 길이가 5이고 높이가 4 인 이등변 삼각형의 밑변을 찾으려면 다음을 연결하고 해결하십시오. 에이2 + 42 = 52. 쉽게 한, 에이2+16=25, 에이2*=9* 그래서 대답은 3. 이 3은 밑면의 절반에 불과하므로 총 밑면은 6입니다.이 삼각형의 넓이를 구하려면 : A = (½)(4)(6)따라서 면적은 12입니다.
이등변 삼각형
특수 이등변 삼각형은 내부 각도가 45, 45 및 90도이며 측면은 서로에 대한 특정 비율입니다. 45-45-90 삼각형의 면적을 구하는 공식은 다음과 같습니다. A = s2 ÷ 2여기서 s는 변의 길이입니다. 측면 길이 중 하나를 제곱 한 다음 제품을 반으로 나눕니다. 예를 들어, 변이 5, 5 및 7 인 삼각형의 면적을 찾으려면 공식은 다음과 같습니다. A = 52 ÷ 2 또는 25 ÷ 12.5. 따라서이 45-45-90 삼각형의 면적은 12.5입니다.