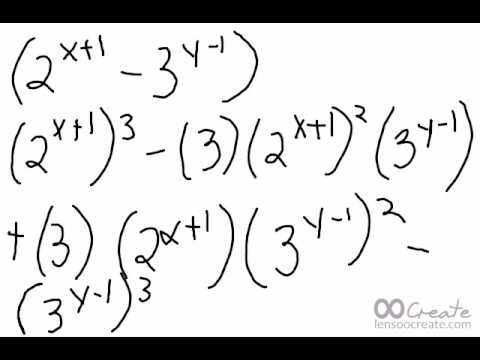
콘텐츠
대수는 매번 산술로 해결할 수있는 반복 패턴으로 가득합니다. 그러나 이러한 패턴은 매우 일반적이기 때문에 일반적으로 계산을보다 쉽게 해주는 몇 가지 공식이 있습니다. 이항의 입방체는 좋은 예입니다. 매번 운동을해야한다면, 연필과 종이를 다듬는 데 많은 시간을 할애해야합니다. 그러나 큐브를 해결하기위한 공식 (및이를 기억하기위한 몇 가지 유용한 트릭)을 알고 나면 올바른 용어를 올바른 가변 슬롯에 연결하는 것만으로 답을 찾는 것이 간단합니다.
TL; DR (너무 길고 읽지 않음)
이항 큐브의 공식 (에이 + 비)는 :
(에이 + 비)3 = 에이3 + 3_a_2비 + 3_ab_2 + 비3
이항의 입방체 계산
당신이 같은 문제를 볼 때 당황 할 필요가 없습니다 (a + b)3 당신의 앞에. 익숙한 구성 요소로 분류하면 이전에 수행했던 더 친숙한 수학 문제처럼 보일 것입니다.
이 경우에는
(a + b)3
와 같다
(a + b) (a + b) (a + b)훨씬 친숙하게 보일 것입니다.
그러나 매번 수학을 처음부터 새로 작성하는 대신 답을 나타내는 수식의 "바로 가기"를 사용할 수 있습니다. 이항 큐브의 공식은 다음과 같습니다.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
공식을 사용하려면 방정식 왼쪽에서 "a"및 "b"의 슬롯을 차지하는 숫자 (또는 변수)를 식별 한 다음 동일한 숫자 (또는 변수)를 "a"및 "b"슬롯으로 대체하십시오. 수식의 오른쪽에.
예 1 : 풀다 (x + 5)3
보다시피, 엑스 수식의 왼쪽에있는 "a"슬롯을 차지하고 5는 "b"슬롯을 차지합니다. 대체 엑스 수식의 오른쪽에 5가 표시됩니다.
엑스3 + 3 배25 + 3x52 + 53
조금 단순화하면 대답에 더 가까이 갈 수 있습니다.
엑스3 + 3 (5) x2 + 3 (25) x + 125
그리고 마지막으로, 최대한 많이 단순화하면 :
엑스3 + 15 배2 + 75x + 125
뺄셈은 어떻습니까?
같은 문제를 해결하기 위해 다른 공식이 필요하지 않습니다. (y-3)3. 당신이 그것을 기억한다면 y-3 와 같다 y + (-3), 문제를 간단히 다시 작성할 수 있습니다. 3 익숙한 공식을 사용하여 해결하십시오.
예 2 : 풀다 (y-3)3
이미 논의했듯이 첫 번째 단계는 문제를 3.
다음으로 이항 큐브에 대한 공식을 기억하십시오.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
당신의 문제에서 와이 방정식의 왼쪽에있는 "a"슬롯을 차지하고 -3은 "b"슬롯을 차지합니다. -3 앞에 마이너스 부호를 유지하기 위해 괄호를 세 심하게주의하여 방정식의 오른쪽에있는 적절한 슬롯에 슬롯을 대입하십시오. 이것은 당신에게 제공합니다 :
와이3 + 3 년2(-3) + 3 년 (-3)2 + (-3)3
이제 단순화 할 시간입니다. 지수를 적용 할 때 음수 부호에 다시 한 번주의를 기울이십시오.
와이3 + 3 (-3) 년2 + 3 (9) 년 + (-27)
한 번 더 단순화하면 답을 얻을 수 있습니다.
와이3 -9 년2 + 27y-27
큐브의 합과 차이를 조심하십시오
지수가 문제가있는 곳에 항상주의를 기울이십시오. 양식에 문제가있는 경우 (a + b)3또는 3여기에서 논의되는 공식이 적합합니다. 그러나 문제가 다음과 같은 경우 (에이3 + b3) 또는 (에이3 -b3)이항의 입방체가 아닙니다. 큐브 (첫 번째 경우) 또는 큐브 차이 (두 번째 경우)의 합입니다.이 경우 다음 공식 중 하나를 적용합니다.
(에이3 + b3) = (a + b) (a2 -ab + b2)
(에이3 -b3) = (a-b) (a2 + ab + b2)