형상에서 3 차원 객체의 하단을베이스라고합니다. 솔리드의 상단이 하단과 평행 한 경우베이스라고도합니다. 베이스는 단일 평면을 차지하므로 2 차원 만 있습니다. 해당 모양의 영역에 대한 공식을 사용하여 밑면의 영역을 찾을 수 있습니다. 정육면체와 정사각형 피라미드에는 정사각형 모양의 밑면이 있습니다. 정사각형의 면적은 측면 중 하나의 길이에 자체를 곱하거나...

원은 자연계와 인간 공학에서 가장 기본적인 형태 중 하나입니다. 구 (또는 구에 근접한 물체, 까다로운 물체) 인 별은 지구와 같은 행성에 생명을 부여 할 수 있습니다. 구의 투영 또는 기하학적 그림자는 원이며,이 두 가지 형태 모두 천문학, 수학, 건축 및 다른 곳에 수많은 영향을 미칩니다. 원은 360도 또는 360 도로 나눌 수 있습니다. 즉, 원 ...

지오메트리를 시작하는 학생들은 원의 면적과 원주를 계산하는 것과 관련된 문제 세트를 경험할 수 있습니다. 원의 반지름을 알고 간단한 곱셈을 수행 할 수있는 한 이러한 문제를 해결할 수 있습니다. 상수 π의 값과 원 속성에 대한 기본 방정식을 배우면 원의 면적이나 원주를 빠르게 찾을 수 있습니다. 원의 원주 또는 면적을 계산하려면 원의 반경을 알아야합니다....

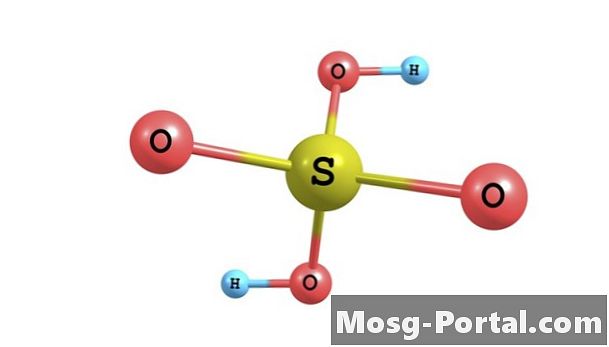
황산은 화학 물질의 산업 생산, 연구 작업 및 실험실 환경에서 일반적으로 사용되는 강력한 무기산입니다. 그것은 분자식 H2O4를 갖는다. 그것은 모든 농도에서 물에 용해되어 황산 용액을 형성합니다. 용액에서, 1 몰의 황산은 음으로 하전 된 설페이트 이온 또는 O4 (2-)의 몰과 2 몰의 양으로 하전 된 하이드로 늄 이온 또는 H3O +로 분리된다. 이들...

일상적인 담화에서 "속도"와 "속도"는 종종 서로 바꿔서 사용됩니다. 그러나 물리학에서 이러한 용어는 구체적이고 뚜렷한 의미를 갖습니다. "속도"는 공간에서 물체의 변위 속도이며, 특정 단위 (초당 미터 또는 시간당 마일)를 가진 숫자로만 주어집니다. 한편, 속도는 방향에 연결된 속도입니다. 그러면 속도...

호는 원의 일부를 이루는 원의 곡선 영역입니다. 원의 호를 아는 경우이 호로 둘러싸인 면적과 원의 중심에서 연장되는 2 개의 선 (두 반지름)을 측정 할 수 있습니다. 이 호 관련 영역을 섹터라고합니다. 이 유형의 계산은 고등학교 또는 대학 기하학 수업이나 조경 또는 공학과 같은 다양한 직업 분야에서 수행해야 할 수도 있습니다. 두 반지름으로 형성된 각도...

큐브는 단순한 모양이며 표면적을 계산하는 간단한 공식이 있다고 가정하는 것이 좋습니다. 정육면체의 모든면의 길이는 같고 모든면의 면적은 같습니다. 큐브에는 6 개의면이 있으므로 한면의 면적을 계산하고 6을 곱하여 총 표면적을 찾으면됩니다. 이 논의에서 나온 수학적 공식은 다음과 같습니다. 길이 L의면을 가진 큐브의 경우 표면적 A = 6L2....

원은 가장 널리 인식되는 기하학적 모양 중 하나이지만 지름과 면적의 수학적 개념을 살펴보면 까다로울 수 있습니다. 둥근 깔개의 크기를 측정하든 둥근 정원이나 안뜰을 지을 공간을 구입하거나 결정 해야하는지, 직경에서 원의 면적을 계산하는 방법을 아는 것은 귀중한 기술입니다. 원의 면적은 원이 차지하는 공간의 양입니다. 원의 넓이를 계산하는 공식은 A = π...

많은 사람들이 다이아몬드 모양이라고 부르는 것에 대한 올바른 이름은 실제로 마름모입니다. 사면은 모든면의 길이가 같고 반대쪽 각도 쌍이 같은 4 면체입니다. 마름모꼴은 연에서 바닥 타일에 이르기까지 모든 곳에 표시되며 해당 마름모에 대한 정보에 따라 다음 세 가지 방법으로 면적을 계산할 수 있습니다. 다이아몬드의 고도와 측면 중 하나의 길이를 곱하십시오....

찰스 다윈의 진화론은 종들이 환경에 적응하기 위해 어떻게 변화 하는가에 관한 것이지만, 삶이 어떻게 시작되었는지에 대한 문제는 다루지 않습니다. 언젠가는 지구가 여전히 뜨겁고 녹 았을 때 지구에는 생명체가 없었지만 나중에 생명이 진화했다는 것을 알았습니다. 질문은 ~이야, 초기 지구 생활 형태는 어떻게 시작 되었습니까?...

정삼각형은 세 변이 모두 같은 길이의 삼각형입니다. 삼각형과 같은 2 차원 폴리곤의 표면적은 폴리곤의 측면에 포함 된 총 면적입니다. 정삼각형의 세 가지 각도도 유클리드 기하학에서 동일한 측정치입니다. 유클리드 삼각형의 각도의 총 측정 값은 180도이므로 정삼각형의 각도는 모두 60 도입니다. 정삼각형의 면적은 그 변의 길이가 알려진 경우 계산 될 수 있습...

이등변 삼각형에는 두 개의 동일한 변이 있습니다. 면적은 삼각형 내 총 공간입니다. 삼각형 화단에 얼마나 많은 뿌리 덮개를 넣을 것인지, A- 라인 건물의 앞면을 덮는 데 필요한 페인트의 양을 결정하거나, 기술을 연마하기 위해 단순히 드릴링 해야하는 경우 삼각형 영역에 알고있는 것을 연결하십시오. 공식. 이등변 삼각형의 면적을 찾으려면 밑면 또는 삼각형의...

곡물 통은 곡물 재배 지역에서 익숙한 광경입니다. 그것들은 어떤 모양이든 될 수 있지만 대부분 원통형이며 원추형 지붕이있는 광대 한 금속 주석처럼 보입니다. 그것들은 이름에서 알 수 있듯이 수확 된 곡물을 저장하는 데 사용됩니다. 크기는 일반적으로 직경이 18 ~ 60 피트이며, 일부는 농업 수명이 다했을 때 주택으로 전환 할 수있을 정도로 큽니다. 빈의 ...

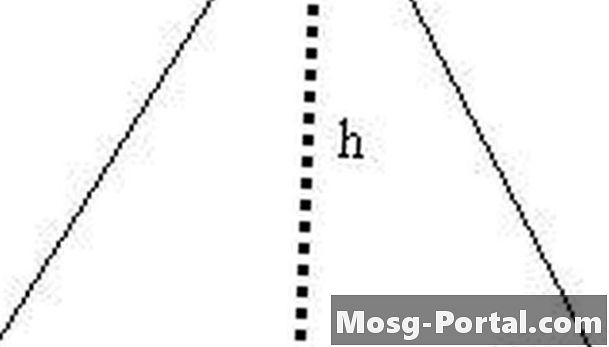
둔각 삼각형은 둔각을 포함하는 삼각형입니다. 90도 이상. 둔각 삼각형의 면적을 구하는 공식은 다른 삼각형과 동일합니다. 면적 = 1/2 x (기본 x 높이). 그러나 둔각 삼각형의 높이는 측면의 높이와 일치하지 않으므로 그림의 높이를 찾는 방법이 다릅니다. 둔각 삼각형의 면적을 계산하려면 먼저 그림의 높이를 찾으십시오. 그림의 밑면을 점선으로 확장하여 ...

육각형은 6 개의 정삼각형으로 구성된 모양입니다. 따라서 삼각형의 면적을 찾아 그 면적을 더하여 육각형의 면적을 계산할 수 있습니다. 삼각형은 정삼각형이므로 한 삼각형의 면적 만 구하고 6을 곱하면됩니다. 육각형 안에 3 개의 선을 그립니다. 육각형의 각 꼭지점 또는 모서리에서 시작하여 반대쪽의 꼭지점을 직선으로 그리십시오. 그 결과 육각형이 6 개의 정...

면적 계산을 처음 시작하면 면적, 원, 삼각형, 정사각형 및 직사각형과 같이 면적을 찾기위한 공식을 명확하게 정의한 쉬운 모양을 얻을 수 있습니다. 그러나 해당 범주에 쉽게 맞지 않는 모양에 직면하면 어떻게됩니까? 미적분학의 용감한 새로운 세계에 들어갈 때까지 불규칙한 모양의 영역을 찾는 가장 좋은 방법은 이미 익숙한 모양으로 세분화하는 것입니다. 불규칙...

수학적 용어로, 타원형-길거나 찌그러진 원처럼 보이는 모양을 타원형이라고합니다. 타원. 이것은 타원의 면적 공식을 사용하여 타원 면적을 찾을 수 있음을 의미합니다. 타원의 면적은 중심을 통과하는 가장 긴 축과 가장 짧은 축의 길이의 절반을 기준으로합니다. 그만큼 중심선 타원의 타원은 타원 중심을 통과하고 타원 가장자리의 반대쪽에있는 두 점을 연결하는 선입...

면적, 둘레 및 부피의 측정은 건설 프로젝트, 공예 및 기타 응용 분야에 중요합니다. 면적은 2 차원 형상의 경계 내부 공간입니다. 둘레는 사각형 또는 원과 같은 2 차원 모양 주위의 거리입니다. 부피는 큐브와 같은 물체가 차지하는 3 차원 공간의 측정 단위입니다. 물체의 크기를 알고 있다면 면적과 부피를 쉽게 측정 할 수 있습니다. 모든 일상적인 기하학적...

파이프의 표면적은 노출 된 파이프 재료의 영역을 나타냅니다. 파이프를 페인트하는 경우 표면 영역을 찾아서 필요한 페인트 양을 추정 할 수 있습니다. 파이프의 표면적을 찾으려면 파이프의 길이와 반경을 알아야합니다. 자로 파이프의 길이를 측정하고 결과 L을 호출하십시오. 파이프의 직경을 측정하고 결과 D를 호출하십시오. 직경은 파이프의 한 측면에서 중심을 통...

초원은 거의 모든 대륙에서 발견 될 수 있으며, 이름에서 알 수 있듯이 가장 풍부한 식생이 초목 인 지역입니다. 온화한 초원은 대초원 또는 대초원으로도 알려져 있으며,이 온화한 초원은 사바나로 알려진 열대 초원보다 온화한 기후를 가지고 있지만,이 생물 군계의 비 생물 적 요인은 나무 대신 잔디와 같은 식물에 적합합니다. ••• Thinktock / Com...